Recent searches
Search options
Is there a math concept that never made sense to you? Which one or ones do you wish someone would explain in new ways?
If none of these come close you can mention something as a comment.
@futurebird Before I read down the thread I didn’t know what ‘the derivitive’ even related to :D My father was an engineer, and obnoxious about Being Right, so I went into visual art where the criticism couldn’t follow.
After he died I went back to school for Comp Sci and had to study up to place out of the intro math class — I like math now, but have still never taken a class more advanced than Algebra II (back in 1977 that was)
@jacquiharper @futurebird Recently I've been casually trying to get a handle on what basic calculus is actually doing.
The derivative is the slope of the graph of a function at a given point. People talk about "rates of change" and "tangents", but no, it's a slope.
Exactly. A “rate of change” is a slope. 20miles/hour is a line with slope 20/1 because, for each 1 hour you go forward in the x-direction, your total total distance goes up by 20 miles in the y-direction.
A tangent is a straight line … again with a slope. So “the slope of a curve at a point” (curves being precisely those lines with non-consonant slopes) we use the tangent to define it in a way so that our straight-line idea of slope works.
@futurebird @Infrapink @jacquiharper
20mph isn't a rate of change; it's a velocity, unchanging.
32 feet per second squared is a rate of change, an accelearation.
A tangent is not a straight line.
https://mathbooks.unl.edu/PreCalculus/tangent-and-cofunctions.html
@phaedral @futurebird @Infrapink @jacquiharper
A tangent is a straight line that touches a curve on exactly one point. The slope of that tangent is then considered the slope of the curve at that exact point.
@dendari @futurebird @Infrapink @jacquiharper Arguably that's a different use of the word. Of course it's been 30+ years since second semester calculus, which is as far as I got.
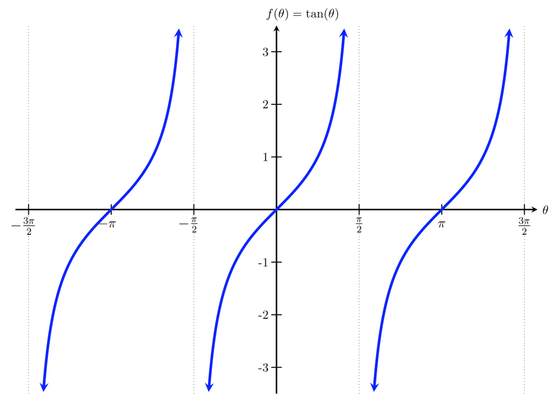
"tangent" is defined:
Given an angle θ (in either degrees or radians) and the (x,y) coordinates of the corresponding point on the unit circle, we define tangent as
tan(θ)=y/x
Resulting in this curve:
@phaedral @futurebird @Infrapink @jacquiharper this is the tangent from trigonometry not the same tangent.
Futurebird is likely a much better math teacher than I am. I haven't done anything beyond 8th grade algebra in years.
@dendari @phaedral @Infrapink @jacquiharper
The crazy thing is... in a way it *is* the same tangent, or at least for a circle.
Most people know that you can plot a circle using:
x=cos theta
y=sin theta
And let theta go from 0 to 2pi (or 0 to 360 if you like)
Because the x and y co-ordinates of a circle are parametrized by the sin and cos.
Tangent has a geometric meaning here too. And this is why it increases without bound as theta gets close to pi/4 (90 degrees)
@futurebird @phaedral @Infrapink @jacquiharper
This is why we need to teach understanding math and not just how to do it.
@futurebird @dendari @Infrapink @jacquiharper Futurebird: I've got a /visual/ that I cannot articulate, for how the line at a tangent to the semi-circle could be used to re-create the trig tangent curve...but if that tangential line is tangential to a curve other than a semi-circle...uh... B^)
@futurebird @dendari @phaedral @Infrapink @jacquiharper
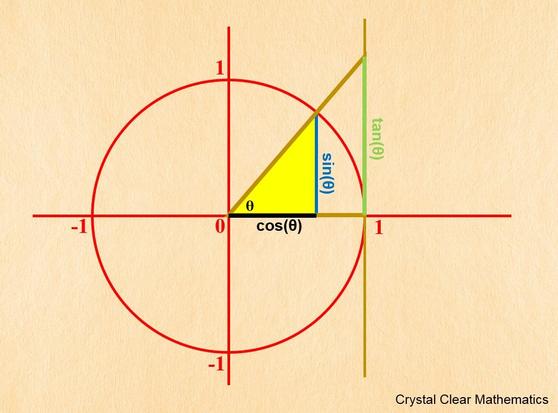
I would like to see a proof that shows that the length of the green line here is always equal to the ratio of the blue line length to the black line length, if you know where I could find one...
@oblomov @futurebird @dendari @phaedral @Infrapink @jacquiharper
Ah, because it's a unit circle! So the "adjacent" side of the big triangle is going to always have a length of 1. And the length of "opposite" side of the big triangle, divided by 1, is equal to the ratio of the opposite side to the adjacent side of the smaller triangle... because they are similar triangles. Thank you!
@futurebird @dendari @phaedral @Infrapink @jacquiharper
Going off on a tangent (ha!), my favorite way of parametrizing a circle of radius 1 is:
x = (1-t^2)/(1+t^2)
y = 2t/(1+t^2)
where t is between -infinity and infinity.
One neat feature is that rational values of t are guaranteed to give you rational values of x and y.
Geometrically, you can think of t as the point where a line pivoting around the point (-1,0) meets the y axis. (x,y) is the point where this line meets the circle.
@dendari @futurebird @Infrapink @jacquiharper I'm totally content with "different tangent," that's sort of what I meant earlier. This has been a /delightful/ exchange!!! Thank you all!!
@dendari @futurebird @Infrapink @jacquiharper Dendari: I see you /teach/ math, so maybe you can help dispel my error.